바쁜 비버
지난 학기에 논리회로 과목을 수강하던 중, 기말고사 시험 문제로 ‘바쁜 비버’에 대한 문제가 출제되었다.
바쁜 비버는 컴퓨터 과학에서 꽤 중요한 개념이다. 특징도 여러 가지 재미있는 게 많아서, 이에 대해 글을 써본다.
본 글의 목차는 다음과 같다.
- 바쁜 비버 게임을 소개한다.
- 바쁜 비버 함수와 최대 시프트 함수를 소개한다. 바쁜 비버 함수의 계산 불가능성을 증명한다.
- 최대 시프트 함수를 중심으로 성질과 하한을 찾아가는 과정을 다룬다. 이 과정에서 아커만 함수, ZF 공리계, 콜라츠 추측과의 연관 관계를 다룰 것이다.
- 바쁜 비버로부터 파생된 함수들을 다룬다.
바쁜 비버 게임
바쁜 비버 게임은 1962년 Tibor Radó의 논문 On Non-Computable Functions에서 처음 소개되었다. Tibor Radó는 컴퓨터 과학에서 많은 업적을 남겼는데, 대부분 튜링 머신과 계산 불가능성에 집중되었다. 이 논문 역시 바쁜 비버 함수의 계산 불가능성(Non-computable)에 대해 다룬다.


이후 바쁜 비버와 튜링 머신에 관한 연구는 T. Radó의 후속 연구인 Computer Studies of Turing Machine Problems(1965)에서 이어진다. 이 논문은 바쁜 비버 게임의 Shift 연산에 대한 논의를 포함하고 있다.
이진 튜링 머신
바쁜 비버 게임을 소개하기 전에, 바쁜 비버 게임이 진행될 이진 튜링 머신(Binary Turing Machine)을 먼저 설정하고 가겠다.
이진 튜링 머신은 S C. Kleene의 Introduction to Metamathematics(1952)에서 소개된 튜링 머신을 일부 변형하여 작동한다.

그렇기 때문에 책에서 소개된 튜링 머신에 대해서 다루어야 하는데, 여느 책에서 소개되는 튜링 머신과 크게 다를 건 없다.
- 셀로 나누어진, 선형의 무한히 긴 테이프
- 유한 개의 상태 중 하나의 상태에 있는 제어 장치
크게 두 장치로 구성되어 있으며, 테이프에서 기호를 읽고 제어 장치의 상태를 변형시킨 뒤, 다시 테이프의 각 셀에 기호를 쓸 수 있다.
튜링 머신 $T=(Q, S, f, q_0)$는 유한 상태 집합 $Q={ q_1, \ldots, q_j}(j\ge 1)$(이때 $q_1$는 시작 상태)와 기호 $S$로 구성된다. $S={s_0, s_1, \ldots, s_k}(k\ge 1)$에서 $s_0$는 공백(blank)를 의미한다.
각 셀은 비어있거나(blank, $s_0$), 유한 개의 기호(symbol, $S$)로 채워질 수 있다. 튜링 머신의 한 동작(move)은 원자적(atomic)적이다.
제어 장치가 현재의 테이프 기호 $s_a$를 읽는다고 해보자.
제어 장치가 상태 $q_c$에 있고, 부분 함수 $f$가 $(q_c, s_a)$에 대해 $f(q_c, s_a)=(q_d, s_b, d)$로 정의될 때 제어 장치는 다음 동작을 한다.
- 상태 $q_c$으로 이동한다.
- 현재 셀에 있는 $s_a$를 지우고 기호 $s_b$을 쓴다.
- $d=R$이면 오른쪽으로 한 칸 이동하고, $d=R$이면 왼쪽으로 한 칸 이동한다. $d=C$이면 가만히 있는다.
이 동작을 기호로 표현하면, 다음 세 가지 형태로 표현할 수 있다:
- $s_bLq_d$
- $s_bCq_d$
- $s_bRq_d$
이진 튜링 머신은 셀에 적힌 기호 $S={0, 1}$인 튜링 머신이다.
다만 바쁜 비버 게임에 사용되는 이진 튜링 머신에는 2가지 차이점을 두었다.
- 먼저 논의를 간편하게 하기 위해, Center Shift($d=C$)를 허용하지 않는다. 따라서 제어 장치의 모든 이동은 “덮어쓰기(overprint)” 이후에 실행된다.
- T. Radó는 상태(state)라는 표현 대신 카드(card)라는 표현을 썼다. 따라서 바쁜 비버 게임을 다루는 본 글에서도 카드라는 표현을 쓸 것이다.
${0, 1} × {L, R}$의 이진 튜링 머신을 만들었으니 바쁜 비버 게임을 소개하겠다.
바쁜 비버 게임
무한히 긴 양방향 테이프를 생각해보자. 테이프의 모든 셀에는 0이 쓰여져 있다. 바쁜 비버 게임은 n개 카드를 갖는 튜링 머신으로 최대한 많은 수의 1을 쓰는 게임이다.
카드가 n개일 때 BB-n 게임이라 하며, BB-n classification에서 가장 많은 1을 쓰는 튜링 머신이 n번째 바쁜 비버가 된다.
한 가지 중요한 전제 조건이 있는데, 튜링 머신은 반드시 정지해야 한다. 그렇지 않으면 무한히 반복되기 때문이다.
게임의 규칙을 살펴보자. 여기서는 카드가 3개인 BB-3를 예시로 설명하겠다.
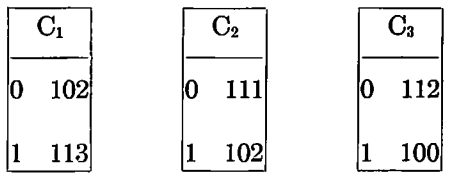
3개의 카드(상태)가 존재하는 튜링 머신을 생각해보자.
- 먼저 플레이어는 n개의 카드를 갖는 이진 튜링 머신을 정의한다. 초기 상태는 Card 1에서 시작하며, 반드시 정지해야 한다.
- 맨 왼쪽 열(1열)에는 ${0, 1}$ 기호가 있다.
- 만약 현재 셀에서 읽은 값이 0이면 윗 행의 동작을, 1이면 아랫 행의 동작을 수행한다.
- 예를 들어 현재 제어 장치의 상태가 $C_1$이고, 현재 셀의 값이 1이면,
113의 동작을 수행한다.
- 그 다음 열(2열)은 “덮어쓸 값(overprint by)” 열이다. 마찬가지로 ${0, 1}$이 올 수 있다.
- 그 다음 열(3열)은 “이동(shift)”할 열이다. 0이면 왼쪽, 1이면 오른쪽으로 이동한다.
- 본 글에서는 편의상 $L$, $R$로 표기한다.
- 마지막 열(4열)은 “다음 카드(call card)” 열이다. 여기서는 제어 장치의 다음 카드의 인덱스 번호가 온다. 0은 정지를 의미한다. 카드가 세 개이므로 ${0, 1, 2, 3}$이 올 수 있다.
A Turing Machine - Busy Beaver 4-state
영상을 보면 이해가 빠를 것이다.
사진에 나와있는 3-카드 튜링 머신의 동작은 아래와 같다(밑줄친 굵은 글씨는 현재 셀의 위치를 나타낸다).
| 단계 | 카드 | 테이프 | 행동 |
| 1 | C1 | 0000000 | 1L2 |
| 2 | C2 | 0001000 | 1R1 |
| 3 | C1 | 0011000 | 1R3 |
| 4 | C3 | 0011000 | 1R2 |
| 5 | C2 | 0011100 | 1R1 |
| 6 | C1 | 0011110 | 1L2 |
| 7 | C2 | 0011111 | 1L2 |
| 8 | C2 | 0011111 | 1L2 |
| 9 | C2 | 0011111 | 1L2 |
| 10 | C2 | 0011111 | 1L2 |
| 11 | C2 | 0011111 | 1R1 |
| 12 | C1 | 0111111 | 1R3 |
| 13 | C3 | 0111111 | 1L0 |
13번의 이동을 통해 6개의 1을 작성하는데, 이는 3번째 가장 바쁜 비버이다.
바쁜 비버 함수
바쁜 비버 함수(라도 시그마 함수)
n개 카드 튜링 머신으로 바쁜 비버 게임을 진행했을 때 쓸 수 있는 1의 개수 최댓값을 $B(n)$으로 표기한다. 이를 바쁜 비버 함수 혹은 라도 시그마 함수(Radó's sigma function) $\Sigma (n)$이라 한다. Radó는 그의 논문에서 $\Sigma (n)$ 표현을 사용했으며, 현대의 논문들은 바쁜 비버 함수를 $BB(n)$으로 표기하기도 한다.
바쁜 비버 함수의 가장 큰 특징으로는, 매우 빠르게 증가하는 함수란 사실이다. 얼마나 빠르게 증가하냐면, $n=5$정도만 되어도 그 값을 알지 못한다.
현재까지 $B(2)=4, B(3)=6, B(4)=13$으로 알려져 있으나, 5 이상의 n에 대해서는 $B(5)\ge 4098$, $B(6)\ge 3.5×10^{18267}$ 임이 알려져 있을 뿐이다.
$B(n)$은 매우 빠르게 증가하는 함수다. 그리고 이로부터 그 어떤 튜링 머신도 충분히 n에 대해 $B(n)$을 계산할 수 없음을, 즉 $B(n)$이 계산 불가능함(Non-computable)을 증명할 수 있다.
일부 컴퓨터 과학을 다루는 한국어 번역본 서적에선 바쁜 비버 함수를 ‘일벌레 함수’라고 번역하기도 한다.
바쁜 비버 함수의 계산 불가능성 증명
모든 n에 대해 BB-n classification의 가장 높은 점수 $B(n)$을 결정할 수 있을까?
이 질문은 바꾸어 말하면 튜링 머신으로 특정한 $n$에 대해 함수 $B(n)$을 계산하는 문제다. 이것이 왜 불가능한 지를 증명해보자.
튜링 머신의 부분 함수 $f(x)$, $g(x)$가 있을 때 특정한 $x_0$보다 큰 $x$에 대해 $f(x) > g(x)$임을 다음과 같이 표현한다:
$$
f(x) > -g(x)
$$
모든 계산 가능한 $f(x)$에 대해 $B(x) > -f(n)$임을 보여 $B(x)$가 계산 불가능함을 보일 것이다.
증명.
$f(x)$를 도입하기 위해 그 보조 함수(Auxiliary function) $F(x)$를 도입한다:
$$
F(x) = \sum_{i=0}^{x}[f(i)+i^{2}]
$$
f(x)가 계산 가능한 함수이므로 F(x)도 계산 가능한 함수이고, 자명하게 다음 성질들이 성립한다
- 성질 1: $F(x) \ge f(x)$ ($\Sigma$ 안에 $f(i)$를 포함하고 있으므로)
- 성질 2: $F(x) \ge x^2$ ($\Sigma$ 안에 $i^2$ 항을 포함하고 있으므로)
- 성질 3: $F(x+1) > F(x)$ (증가함수이므로)
$F(x)$가 계산 가능하므로, $F(x)$를 계산하는(부분 함수로 갖는) n-카드 이진 튜링 머신 $M_F$를 설정한다.
그리고 임의의 양의 정수 $x$에 대해 $x+1$ 카드 이진 튜링 머신 $M^{(x)}$를 설정한다. 이 튜링 머신은 테이프에 $x+1$개의 연속된 1을 출력한 후 정지한다.
예를 들어 $x=2$에 대해 $M^{(2)}$는 다음 3-Cards를 갖는다:
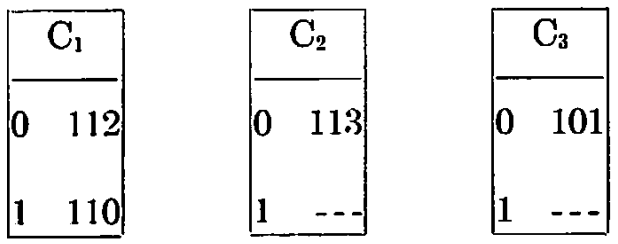
이제 새로운 이진 튜링 머신 $M_F^{(x)}$을 도입하자. 이 튜링 머신은 $M^{(x)}$를 시작하여 $M_F$를 실행시키고, 다시 $M_F$를 실행하는 일련의 동작을 수행한다.
$$
M_{F}^{(x)} : M^{(x)} \rightarrow M_F \rightarrow M_F
$$
이때 $M^{(x)}$의 카드 수는 $x+1$, $M_F$의 카드 수는 C이다. $M_F^{(x)}$가 $M^{(x)}$와 2개의 $M_F$로 이루어져 있기에 $M_F^{(x)}$의 카드 수는 $1+x + 2c$이다.
$M_F^{(x)}$의 All-Zero 테이프에서 출발한다.
- 먼저 오른쪽 방향으로 $x+1$개의 연속된 1을 출력한다.
- 또다시 0이 나오면 그 오른쪽에 다시 연속된 $F[F(x)]+1$개의 1을 출력한다.
- 마지막으로 가장 오른쪽에 출력한 1 아래에서 멈춘다.
$M_F^{(x)}$를 통해 구성된 이진 튜링 머신은 $B(1+x+2C)$에서의 동작에 해당된다. 곧 $T_F^{(x)}$는 $B(1+x+2c)$의 상한에 대한 항목이며($BB-(1+x+2C)$ Classification), 그 점수는 $3+x+F(x) + F[F(x)]$이다.
따라서 이 Classification의 최대 점수 B(1+x+2C)는 다음을 만족한다(부등식 1):
$$
B(1 + x + 2C)\ge 3 + x + F(x) + F[F(x)]
$$
여기서 자명하게 $x^2 > - (1+x+2C)$이고, 성질 2에서 $F(x) \ge x ^ 2$이므로
$$
F(x) > - (1+x+2C)
$$
또한 성질 3에서 F(x)가 단조 증가하므로 바로 위 식에서(부등식 2):
$$
F[F(x)] > - F(1 + z + 2C)
$$
를 끌어낼 수 있다.
_부등식 1, 2_에서:
$$
B(1 +x + 2C) > - F(1 + x + 2C)
$$
$F(x) \ge f(x)$이므로
$$
B(1 +x + 2C) > - f(1 + x + 2C)
$$
$n=1+x+2C$를 대입하면
$$
B(n) > -f(n)
$$
을 얻는다. 곧 $B(n)$은 그 어떤 계산 가능한 함수 $f(n)$보다 크므로 $B(n)$은 계산 불가능하다.
최대 시프트 함수
최대 시프트 함수(미친 개구리 함수)
최대 시프트 함수 $S(n)$은, BB-n Classification에서의 최대 이동 횟수에 대응한다. 미친 개구리 함수 $FF(x)$라 하기도 한다.
$k$개의 1을 쓰기 위해서는 적어도 $k$번 이상의 이동(Shift)을 거쳐야 하므로 자명하게 $S(n) \ge B(n)$이 성립한다.
앞에서의 증명과 비슷한 과정으로 모든 계산 가능한 함수 f(n)에 대해 $S(n) > -f(n)$임을 보일 수 있고, 따라서 최대 시프트 함수 역시 계산 불가능하다.
Aaronson 교수 등 바쁜 비버 함수를 연구한 현대의 많은 이들은 최대 시프트 함수 $S(n)$을 바쁜 비버 함수 $BB(n)$으로 바꾸어 부르기도 한다. 그러나 본 글에서는 Radó가 처음 제시한 표현을 따르겠다.
Radó는 1962년의 논문에서 최대 시프트 함수의 정의에 대해서만 제시하고, 그에 대한 자세한 연구는 1965년 Computer Studies of Turing Machine Problems에서 진행되었다.
최대 시프트 함수에 대한 논의는, BB-n Classification에서 가장 많은 1을 쓰는 튜링 머신은 하나가 아닌, 여러 개가 존재할 수 있다는 점에서 출발한다. 예를 들어 BB-3 Classification에서 6개의 1을 적는 튜링 머신은, 위에서 소개한 튜링 머신 이외에 여러 개가 있다.
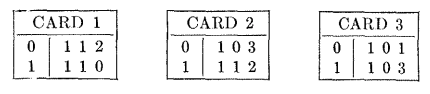

위 튜링 머신(2) 오른쪽 그림과 같은 과정을 거치며 6개의 1을 쓴다.
아래 그림은 튜링 머신(1), (2) 이외에 6개의 1을 쓰는 또다른 튜링 머신을 나열한 것이다.
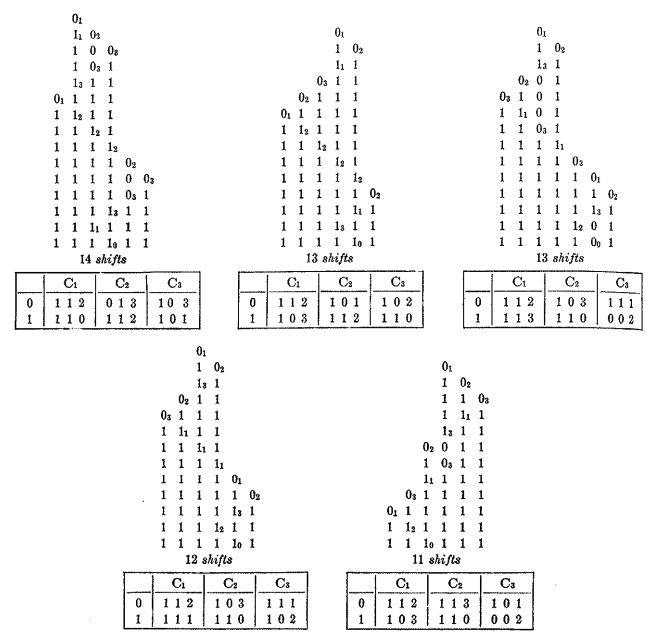
주목해야 할 점은 1을 쓰기 위해서, 몇 번의 이동(Shift) 연산을 거쳐야 하는 지다. 같은 6개의 1을 쓰더라도, 이동 연산의 횟수가 모두 다르다.
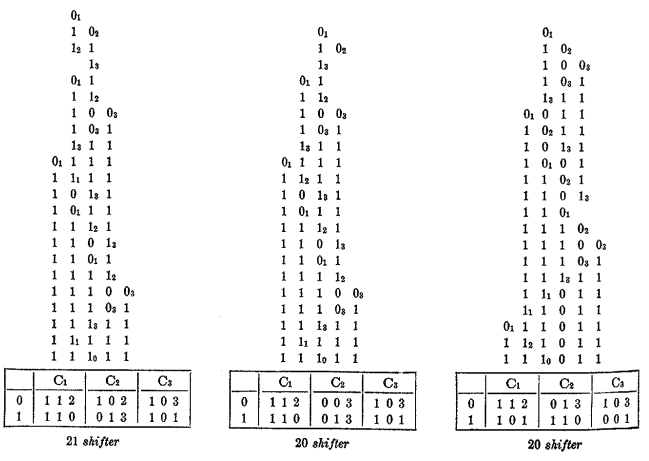
만약 6개의 1을 포기한다면, 더 많은 이동 횟수를 갖는 튜링 머신을 확인할 수 있다.
위 그림은 5개의 1을 쓰며, 20 이상의 이동 횟수를 갖는 튜링 머신의 예시다.
여기서 알 수 있듯 최대 시프트 함수와 바쁜 비버 함수가 갖는 튜링 머신은 서로 다를 수 있다. 예컨대 BB-3 Classification에서 $B(3) = 6$, $S(3) = 21$이지만, 21번의 이동 연산을 통해 6개의 1을 찍는 튜링머신은 존재하지 않는다.
최대 시프트 함수의 엄밀한 정의
최대 시프트 함수 $S(n)$을 엄밀히 정의해보자.
튜링 머신 $M$에 대해, M이 초기 all-0 테이프에서 실행될 때 $s(M)$을 M이 정지하기 전까지 Shift Step의 수로 정의하자. 이때 마지막 정지 STEP도 포함된다.
만약 M이 정지하지 않는다면 $s(M)\coloneqq\infty$로 표기한다.
한편 n 카드 이진 튜링 머신 $T(n)$을 생각해보자. 이때 $|T(n)| = (4n+1)^{2n}$이 성립한다 (Radó는 이 증명을 생략했다).
이를 계산하면 각각의 n-카드 머신을 $n\log_{2}n + O(n)$ 개의 비트를 이용해 특정할 수 있다.
그렇다면 $S(n)$을 아래와 같이 정의할 수 있다:
$$
S(n)\coloneqq \max_{M\in T(n) : s(M) < \infty} s(M)
$$
이는 양의 정수 n에 대해 성립한다.
최대 시프트 함수와 바쁜 비버 함수와의 관계
자명하게 $S(n) \ge B(n)$이 성립하지만, 현대에서는 더 구체적인 관계성을 확인했거나 추정하고 있다.
2002년 Ben Amram과 Petersen은 바쁜 비버 함수를 이용해 최대 시프트 함수의 상한을 제시했다.
$$
\exists c \text { s.t. } \forall n : S(n) < B(n+8\lceil \frac{n}{\log_2 n}\rceil + c)
$$
이는 2024년 현재까지 확인된 최대 시프트 함수의 가장 강한 상한이기도 하다.
더 나아가서 Aaronson은 2020년, 추정이기는 하나 더 구체적인 상한을 제시했다:
$$
\forall n \ge4: S(n) <B(n+1)
$$
이는 $n\ge 4$일 때 성립되는 데, 현재까지 확인된 바로는 $n = 3$일 때 $S(3) = 21$, $B(4) = 13$에서 거짓인 것 외에는 모두 성립된다고 한다.
동시에 그는 더 과감한 추정을 제시했다. $S(n)\approx B(n)^2$이 성립한다는 추정이다. 즉 다시 말해:
$$
\lim_{n\to\infty} \frac{\log S(n)}{\log B(n)} = 2
$$
가 성립한다는 추측이다.
하한과 특징
본 차례에선 최대 시프트 함수를 주인공으로 삼고 있지만, 바쁜 비버 함수(라도 시그마 함수)에도 동일하게 적용된다.
아커만 함수와의 비교
최대 시프트 함수 $S(n)$의 더 일반적인 하한은 알려져 있다. $n$이 작을 때만 유의미한 약한 하한이기는 하나, 1964년 Green은 아커만 함수(Ackermann function) $A$에 대해, $n\ge 2$에서 $S(2n) \ge A(n-2)$ 임을 보였다.
아커만 함수는 1928년 빌헬름 아커만(Wilhelm Ackermann)이 발표한 함수이다. 바쁜 비버 함수 이전에 폭발적으로 증가하는 함수의 대표격이었다. 재귀의 깊이가 매우 깊어 m, n이 4 이상 정도만 되어도 값이 매우 커지는 함수다.
$$
A(m, n) = \begin{cases}
n+1 &\quad\text{if } m=0, \\
A(m-1, 1) &\quad\text{if } m>0\text{ and } n=0\\
A(m-1, A(m, n-1))&\quad\text{if } m>0 \text{ and } n>0
\end{cases}
$$
아커만 함수 역시 매우 빠르게 증가하는 함수인데, 최대 시프트 함수는 이보다 훨씬 폭발적으로 증가한다는 의미다.
공리계
아커만 함수를 통한 일반적인 하한을 알았지만, 그보다 더 구체적인 하한을 알 수는 없을까?
이에 대한 많은 연구가 진행되었다. 몇 가지 주요한 연구를 살펴본다.
ZF - SRP 공리계
Aaronson 정리: ZF + SRP (SRP는 Stationary Ramsey Property의 약자) 집합 이론이 모순되는 경우에만 멈추는 "명시적인" 7910-카드 튜링 머신이 존재한다. 즉, 집합 이론이 모순이 없다면, ZF 공리계는 S(7910)의 값을 증명하지 못한다.
놀랍게도 이게 증명이 된다! 분명 $S(7910)$은 하나의 존재하는 숫자이다. 그리고 가능한 7910-카드 튜링 머신은 유한 개이고, 그 중 일부는 영원히 돌아가고, 일부는 정지한다. 그 정지하는 기계들 중 가장 길게 돌아가는 특정한 기계가 존재할 것이다.
Aaronson과 Adam 교수는 널리 사용되는 ZF 공리계 안에서, S(7910)이라는 정확한 값을 증명하는 것이 본질적으로 불가능함을 보였다(7910이 아니라 8000, 8001 등 더 큰 숫자도 마찬가지다).
이걸 어떻게 증명했을까?
먼저 7910 카드 튜링 머신을 손수 만든다. 이들은 이 튜링 머신을 만들기 위해 ‘Laconic’이라고 하는 특수한 프로그래밍 언어를 직접 만들었다. 이 튜링 머신은 ZF 공리계에서 나올 수 있는 결과들을 하나하나 나열하고, 모순을 발견하는 경우(0=1을 보이는 경우)에만 멈추는 기계이다.
집합론에 일관성이 있다면, 즉 ZF 공리계가 모순이 없이 참이라면, 프로그램은 영원히 실행될 것이다. 만약 프로그램이 영원히 실행된다는 것을 증명한다면, 이는 곧 ZF 집합론의 일관성을 증명하는 것과 같다.
그리고 이것이 불가능하다는 정리가 바로 괴델의 불완전성 정리이다.
괴델의 증명에 따르면 A라는 집합론이 있을때, A만을 갖고서 A의 일관성을 증명하지 못한다. 다시 말해 위의 프로그램이 영원히 돌아가는 지, 혹은 멈추는 지를 ZF 공리계를 갖고 증명하지 못한다.
이미 한 집합론 내에서 알아낼 수 있는 바쁜 비버 함수의 값이 유한 개라는 것은 알려져 있었다. 이들은 고도의 최적화와 공학적 기술을 통해(특수한 인코딩 기법을 사용했다), 그 값이 8000보다 아래라는 것을 알아냈다.
ZF 공리계
그 이후에 Stefan O’Rear는 이 값을 1919로 내렸고, 이후에는 748-카드 튜링 머신까지 증명했다.
O’Rear 정리: ZF 집합 이론이 모순되는 경우에만 멈추는 명시적인 748-카드 튜링 머신이 존재한다. 즉, 집합 이론이 모순이 없다면, ZF 공리계는 S(748)의 값을 증명하지 못한다.
O’Rear는 Laconic 언어와, Aaronson이 사용한 인코딩 기법을 재활용했다. 여기서 더 나아가 Friedman의 ZF + SRP 이론에서 벗어나, SRP에 대한 의존성을 제거하고 ZF 공리계에 직접 접근하여 연구를 진행했다.
골드바흐의 추측
Code Golf Addict라는 github 유저는 다음을 증명했다(링크):
Code Golf Addict의 증명: 골드바흐의 추측이 거짓이라면 멈추는 명시적인 27-카드 튜링 머신이 존재한다.
그 이전에 Jared Showalter는 같은 내용의 47-카드 튜링 머신을 증명했는데, 여기에 더 자세한 설명이 담겨있다: https://gist.github.com/jms137/cbb66fb58dde067b0bece12873fadc76
리만 가설
Matiyasevich, O’Rear, Aaronson은 다음을 증명했다(링크):
Matiyasevich, O’Rear, Aaronson의 증명: 리만 가설이 거짓이라면 멈추는 명시적인 744-카드 튜링 머신이 존재한다.
그 외 추정
위의 내용은 이미 증명된 사실이다.
Aaronson 교수는 여기서 더 나아가서 많은 추정들을 제시한다.
현재까지 $S(5)$의 값은 증명되지 않았지만, 1990년 Marxen과 Buntrock이 발견한 47176870번의 스텝이 $S(5)$의 값일 거라는 추정이 있다.
반대로 $S(6)$, $S(7)$ 등 6 이상부터는 그 값을 영원히 알지 못할 것이라 추측된다.
Aaronson의 최대 시프트 함수 추정: $S(5)=47176870$이다. $n\ge 6$부터는 $S(n)$의 값을 알 지 못 한다.
한편 ZF 집합론에서 증명 불가능한 $S(n)$에 대해 최소의 n값은 얼마일까? 위에서 Aaronson은 이미 $S(748)$을 증명하지 못함을 보였다. 그는 ZF 공리계가 $S(20)$을 증명하지 못할 것이라 추정한다.
콜라츠 추측
콜라츠 추측(Collatz Conjecture)이란 게 있다. 함수 $f:\mathbb{N}\to \mathbb{N}$에 대해
$$
f(x) = \begin{cases}
\cfrac{x}{2} &\quad\text{if } x \text{ is even} \\
3x+1 &\quad\text{if } x \text{ is odd}
\end{cases}
$$
가 있을 때, 모든 양의 정수 $x$에 대해 $(f(x), f(f(x)), \ldots)$로 유한 번 재귀 반복하면 1로 간다는 추측이다.
예를 들어 5에서 시작하면
$$
5\to 16 \to 8\to 4\to2\to1
$$
이 된다. 1에 도달한 이후에는 $4\to2\to1$을 반복한다.
이 추측은 현재까지 증명되지 않았지만, $x\le 2^{68}$까지 성립한다.
놀랍게도 바쁜 비버 튜링 머신 역시 콜라츠 수열과 비슷한 양상을 보인다.
위에서 Marxen과 Buntrock이 발견한 5번째 바쁜 비버 튜링 머신도 그 예시이다.
해당 튜링 머신의 동작을 함수로 표현하면 아래와 같이 표현할 수 있다고 한다.
$$
g(x) \coloneqq
\begin{cases}
\cfrac{5x+18}{3} & \quad\text{if } x \equiv 0\pmod{3} \\
\cfrac{5x+22}{3} & \quad\text{if } x \equiv 1\pmod{3} \\
\perp & \quad\text{if } x \equiv 2\pmod{3}
\end{cases}
$$
질문: 만약 $x=0$에서부터 시작해서 $x\coloneqq g(x)$를 재귀적으로 반복한다면 결국 $\perp$ 상태에 도달할까?
0 → 6 → 16 → 34 → 64 → 114 → 196 → 334 → 564
→ 946 → 1584 → 2646 → 4416 → 7366 → 12284 → ⟂
정답은 도달한다이다.
5-카드 튜링 머신은 Marxen-Buntrock 머신 외에, 6-카드 튜링 머신인 Kropitz의 튜링 머신도 콜라츠 수열과 유사한 동작을 한다고 알려져있다.
이처럼 $n$이 낮은 수일 때, 바쁜 비버 튜링 머신은 콜라츠 수열과 비슷한 양상으로 행동한다. 이를 토대로, John Conway는 콜라츠 수열의 일반화된 버전이 튜링 결정불가능(Turing-Undecidable)함을 증명했다.
바쁜 비버 함수에 대한 연구가 콜라츠 수열에 대한 연구에도 영향을 주고 있음을 알 수 있다.
파생 함수
고차 바쁜 비버 함수
지금까지 바쁜 비버 함수, 최대 시프트 함수가 아득히 초월적인 양상으로 빠르게 증가한다는 것을 알았다.
그러나 이런 바쁜 비버들조차 우습게 만드는, 더 강력한 시스템이 있을까?
$B(n)$, $S(n)$은 튜링 머신으로 계산이 불가능한 함수다. 그러나 계산 가능성 이론에서는 어떤 $n$에 대해 $B(n)$, $S(n)$을 바로 출력하는 마법의 상자를 생각해볼 수 있다. 이 상자를 ‘오라클(Oracle)’이라 부른다.
오라클은 현실에는 존재하지 않는, 마법적인 능력의 슈퍼 튜링 기계이다. 그렇다면 슈퍼 바쁜 비버 함수 $SBB(n)$을 n 카드 슈퍼 튜링 기계가 중지하기 전 시행하는 최대 시행 수(여기서는 최대 시프트 함수의 초월을 의미)로 정의할 수 있다.
이 슈퍼 바쁜 비버 함수 $SBB(n)$은 그 어떤 슈퍼 튜링 머신으로 계산할 수 있는 함수보다도 빠르게 증가한다. 예컨대 $B(n)$, $B(B(n))$보다 빠르게 증가한다.
그렇다면, 슈퍼 바쁜 비버 함수를 오라클로 쓸 수 있는 튜링 머신을 생각해보자. 이를 슈퍼 울트라 튜링 머신이라 해보자. 이를 반복하면 슈퍼 울트라 튜링 머신으로 슈퍼 울트라 짱짱맨 튜링 머신을 정의할 수 있고, 슈퍼 울트라 짱짱맨 튜링 머신으로 슈퍼 울트라 짱짱맨 원더풀 튜링 머신을 정의하고, 이를 무한히 반복할 수 있다.
💡 Scott Aaronson의 글 Who Can Name the Bigger Number?에서 쓰인 표현을 그대로 쓴 것인데, 원문은 각각 Super Turing machine, super duper machine, super duper pooper machine으로 번역되었다.
더 강력한 튜링 머신을 정의하기 위한, 이러한 계층구조는 1943년 Kleene에 의해 만들어졌다.
물론 Kleene가 'Super duper pooper'나 '울트라 짱짱맨'같은 단어를 쓰진 않았다.
대신 $B_1(n)$, $B_2(n)$, $B_3(n)$과 같은 표현을 쓸 수 있다. $B_1(n)$을 보통의 바쁜 비버 함수라 한다면, 2차 바쁜 비버 함수 $B_2(n)$은 $B_1(n)$을 이용해 정의된 함수이고, 3차 바쁜 비버 함수 $B_3(n)$은 $B_2(n)$으로 정의된 함수이다. 곧 n차 바쁜 비버 함수를 정의할 수 있다.
수 체계를 확장한다면, ω차 바쁜 비버 함수 $B_\omega(n)$을 생각해볼 수 있다. 이때 ω는 첫 번째 무한 서수(the first infinite ordinal, 첫 번째 서수)이다. 서수란 무한 집합까지 포함한 이름지을 수 있는 모든 숫자의 집합에서, 그 모든 것보다 더 큰 숫자로 가는 수 체계의 일종이다. $B_\omega(n)$은 모든 자연수 $k$에 대해 $B_k(n)$을 오라클로 쓸 수 있는 튜링 머신을 통해 정의된 바쁜 비버 함수다.
멈추지 않고 더 나아갈 수 있다. $B_\omega (n)$을 오라클로 쓰는 튜링 머신으로 $B_{w+1}(n)$을 정의할 수 있고, $B_{w+2}(n)$, $B_{w+3}(n)$ 등을 정의할 수 있다. 이를 무한히 반복하면 모든 자연수 k에 대해 $B_{w+k}(n)$을 오라클로 쓸 수 있는 튜링 머신을 통해 정의된 2ω차 바쁜 비버 함수 $B_{2\omega}(n)$을 정의할 수 있다.
$B_{3\omega}(n)$, $B_{4\omega}(n)$ 등을 반복하면 모든 자연수 k에 대해 $B_{k\omega}(n)$을 오라클로 쓸 수 있는 튜링 머신을 통해 정의된 $\omega ^ 2$차 바쁜 비버 함수 $B_{\omega ^2}(n)$을 정의할 수 있고, $B_{\omega ^3}(n), B_{\omega ^ 4}(n), \cdots, B_{\omega^k}(n)$를 통해 $\omega^{\omega}$차 바쁜 비버 함수, $\omega^{\omega^{\omega}}$차 바쁜 비버 함수 등을 정의할 수 있다. ω가 ω번 반복되는 $\omega^{\omega^{\omega^{\dots}}}=\varepsilon_0$에 대해 $B_{\varepsilon_{0}}(n)$에 도착할 수도 있다. 각 함수는 오라클로 쓰이는 그 이전 함수보다 더 빠르게 증가한다.
언뜻 보면 ‘손오공에서 전투력 숫자 싸움’이나, ‘타노스보다 쎈 캉’처럼 아무 의미 없는 숫자 싸움으로 보일 수 있다. 하지만 서수를 통해 초월성의 개념을 체계화할 수 있고, 이러한 체계의 확장은 수학적 본질에도 맞닿아 있다고 믿는다.
한편 이러한 확장 역시 무한하지는 않다. 다음 서수로 확장하기 위해서는 공리계에서 그 서수가 존재함을 증명할 수 있어야 한다. 한 공리계에서 서수의 확장은 한계가 존재한다. 언젠가는 연료가 떨어진다.
더 강력한 공리계를 상정한다면, 더 큰 서수가 존재함을 증명할 수 있다. 반대로 더 큰 서수를 증명할 체계를 고안하지 않으면, 더 이상의 초월은 불가능해진다. 끝이 보이지 않는 싸움인 줄 알았지만, 결국에 이 역시 괴델의 늪에 봉착한다.
가령 ZF 집합론에서 증명 가능한 가장 큰 서수 $\omega_{\text{ZF}}$에 대해 $B_{\omega_{\text{ZF}}}(n)$이 ZF에서 상상 가능한 가장 큰 비버 함수라 볼 수 있겠다.
한편 $\omega(n)$을 n-카드 튜링 머신에 의해 계산 가능한 모든 서수의 최상위값으로 정의한다면, $F(n)\coloneqq B_{\omega(n)}(n)$로 정의할 수 있다. 이는 모든 계산 가능한 서수에 대해 새로운 함수를 정의할 수 있음을 의미한다.
삑삑거리는 바쁜 비버 함수(Beeping Busy beaver function)
2차 바쁜 비버 함수 $B_2(n)$의 초기 값을 구하기 위해 정의된 함수다. Aaronson과 Friedman이 연구했다.
바쁜 비버 함수와 동작은 유사한데, 대신 미리 정해진 특정한 상태를 벗어날 때 ‘beep’ 소리를 낸다. 이를 ‘beep state’라 한다.
beeping TM M에 대해 M이 초기 all-zero tape에서 시작할 때, $b(M)$을 M이 beep 소리를 내기까지 스텝 횟수라 할 때(만약 M이 무한번 소리내면 $b(M)\coloneqq\infty$) n 번째 삑삑거리는 바쁜 비버 $BBB(n)$은 다음과 같이 정의된다.
$$
BBB(n)\coloneqq \max_{M\in T(n) : b(M) < \infty}b(M)
$$
$BBB(n)\ge S(n)$ 관계이고, n이 커질 수록 BBB는 S(n)과 비교해서 기하급수적으로 빠르게 증가한다.
$BBB(1)=1, BBB(2)=6$임이 알려져 있으며
| A | B | C | |
| 0 | 1LB | 1RA | 1RC |
| 1 | 0RB | 0LC | 1RA |
위 튜링머신으로 확인했을 때
$$
BBB(3) \ge 55 > S(3) =21
$$
임이 알려져 있다.
세미 바쁜 비버 함수(Semi-Busy beaver function)
바쁜 비버 함수보다는 느리지만, 여전히 모든 계산 가능한 함수보다도 빠르게 증가하는, 중간에 위치한 함수다.
- 모든 계산 가능한 함수 $f$에 대해 $\exists n_f \text{ s. t. } \forall n\ge n_f : g(n) > f(n)$이지만
- $g$의 오라클에 대해 여전히 계산 불가능한, 정지하는(혹은 바쁜 비버와 동치인)
함수 $g:\mathbb{N}\to\mathbb{N}$이 존재함을 보이자.
증명:
$\mathbb{N}\to\mathbb{N}$ 함수 $f_1, f_2, \ldots$를 모든 계산 가능한 함수를 열거한 것이라 하자. 무한히 증가하는 비감소 함수 $\omega :\mathbb{N}\to\mathbb{N}$에 대해
$$
g(n) \coloneqq \max_{i\le \omega(n)} f_i (n)
$$
을 정의하자. g는 이미 모든 계산 가능한 함수 $f_i$보다 커질 것이므로 위에서 (1)을 만족한다. 이제 (2)를 만족시킬 ω를 골라보자.
튜링 머신 $R_1, R_2, \ldots$를 HALT에서 g로 가는 후보들의 축소(Reduction)를 열거한 것이라 하자. 그렇다면 아래 과정을 반복하여 ω를 만들 수 있다.
- $\omega(1) \coloneqq 1$이라 한다.
- 각 $n=1, 2, 3,\ldots$에 대해
- 머신 $R^{g}_{w(n)}(x)$이 n 이하의 값에 대해서만 g를 쿼리하게끔 하는 $x \in {0, 1}^*$가 존재하고,
- $x\in \text{HALT}$인지 정확하게 결정하는 것에 실패한다면
- $\omega(n+1)\coloneqq \omega(n)+1$로 한다.
- 그렇지 않다면, $\omega(n+1)\coloneqq \omega(n)$로 한다.
ω는 무한대로 증가한다고 가정하면, 증명하고자 하는 (2)를 만족한다. 모든 HALT에서 g로의 가능한 Reduction을 제거하기 때문이다.
그렇다면 ω가 무한대로 증가함을 보이자. 이를 보이기 위해선 우선 어떤 고정된 값 $\omega^{*}$에 대해 $\omega(n)$이 증가하지 않는다면, $g$가 계산 가능하다는 것을 생각해보자. $R^{g}_{w^*}$는 모든 입력에 대해 HALT할 것이다. 그러므로 HALT는 계산 가능하다. 실제론 HALT는 계산 불가능하다. 이는 모순이므로 곧 ω는 무한대로 증가한다.
차분한 오리너구리 함수(Placid playtpus function)
$B(n) \ge n$이라는 것은 자명하다. n 카드 튜링 머신이 n개의 1을 출력한 후 정지하는 상황을 생각해보라.
Boolos와 Jeffrey는 주어진 n 카드 튜링 머신을 갖고, 원래 기계가 출력하는 1의 문자열 길이의 두 배를 생성하는 튜링 머신을 연구했다. $B(n+7) \ge 2n$, 즉 n 카드 튜링 머신이 m개의 1을 출력할 때, n+7k 카드의 튜링 머신이 $m × 2^k$개의 1을 쓴다는 것을 밝혔다.
더 나아가 Dewdney는 1993년 $B(n) \ge 2^n$임을 주장했다. 즉 m개의 1을 쓰기 위해 필요한 카드의 개수는 최대 $\log_2 m$개를 넘지 않는다는 의미다.
이러한 전개는 “n개의 1을 쓰기 위해 필요한 최소한의 카드 개수는 무엇인가?”라는 질문으로 이어진다. 이에 대한 함수를 차분한 오리너구리 함수(Placid playtpus function) $PP(n)$이라 한다.
차분한 오리너구리 함수는 바쁜 비버 함수와 역함수 관계이다.
$$
PP^{-1}(n) = BB(n)
$$
곧 m개의 1을 출력하는 n 카드 튜링 머신이 있을 때 $BB(n) \ge m$과 $PP(m) \le n$을 동시에 만족한다.
아커만 함수의 역함수와 마찬가지로, $BB(n)$이 매우 빠르게 증가하는 만큼 $PP(n)$ 역시 매우 느리게 증가한다. ‘우주적으로’ 큰 수를 집어넣어도 매우 작은 결과가 튀어나오며, 계산 불가능한 함수의 역함수이기에 $PP(n)$ 역시 계산 불가능하다.
그럼에도 불구하고 $PP(n)$ 역시 증가하는 함수이며, $\displaystyle\lim_{n\to\infty} PP(n) = \infty$이다(단지 매우 느리게 증가할 뿐이다).
피곤한 웜뱃 함수(Weary wombat function)
최대 시프트 함수에도 똑같은 논리로, n번의 이동 연산을 위해 필요한 최소한의 카드 개수를 피곤한 웜뱃 함수(Weary wombat function) $WW(n)$으로 정의한다. $WW(n)$은 $S(n)$의 역함수이다.
$$
FF^{-1}(n) = S(n)
$$
한편 차분한 오리너구리 함수, 피곤한 웜뱃 함수의 초기 값들은 대략적으로 구해져있다.
| n | $PP(n)$ | $WW(n)$ |
| 4 | 2 | 4 |
| 5 | 3 | 7 |
| 6 | 3 | 11 |
| 7 | 4 | 12 |
| 8 | 4 | 14 |
| 9 | 4 | 19 |
| 10 | 4 | 30 |
| 11 | 4 | 40 |
| 12 | 4 | 53 |
| 13 | 4 | 96 |
| 14 | 5 | ≤ 41 |
| 15 | 5 | ≤ 45 |
마치며
이번 글을 통해 바쁜 비버 함수에 대한 여러 내용을 간단히 살펴보았다.
바쁜 비버 함수에 대한 연구는 현재도 계속되는 중인데, 이중 많은 부분은 수 이론(Number Theory)와 연관되어 있어서, 글을 쓰는 데 있어 어려운 점도 있었고, 특히 서수에 관한 부분은 이해를 포기했다...
한편 여전히 현대의 컴퓨터과학자들이 답하지 못하는 질문들도 많다. 가령 $S(6)$, $B(7)$과 같은 값은 짝수인가, 홀수인가라는 질문 등이다.
계산 가능성에 대한 질문은 컴퓨터의 근본적인 능력에 대한 질문에도 맞닿아 있다.
이 글은 바쁜 비버에 대한 자세하거나 엄밀한 내용을 다루고 있지 않다. 이에 대해 더 자세히 알고 싶다면, 아래 References를 확인해보라.
📚 References
- Aaronson, S. (2020). The busy beaver frontier. ACM SIGACT News, 51(3), 32-54.
- Aaronson, S. Who Can Name the Bigger Number? Shtetl-Optimized.
- Fu, L. E., & Pan, S. (2022). The Busy Beaver Problem.
- Harland, J. (2006, January). The Busy Beaver, the Placid Platypus and other Crazy Creatures. In CATS (Vol. 6, pp. 79-86).
- Hhan. (2020, June 1). 큰 숫자들 by Scott Aaronson. PSEUDORANDOM THINGS.
- Kleene, S. C. (1952). Introduction to metamathematics. Princeton, N. J.: D. Van Nostrand Co.
- Lin, S., & Rado, T. (1965). Computer studies of Turing machine problems. Journal of the ACM (JACM), 12(2), 196-212.
- Rado, T. (1962). On non‐computable functions. Bell System Technical Journal, 41(3), 877-884.
- Rosen, K. H. (2020). Rosen의 이산수학 (정진우, 역.; 8th ed.). McGraw-Hill Education Korea, LTD.

